correlacion

La covarianza también se utiliza para calcular una medida estandarizada de la variabilidad
conjunta llamada correlación.

"Si dos variables aleatorias son estadísticamente independientes, la covarianza entre ellas
es 0. Sin embargo, lo contrario no es necesariamente cierto. La razón por la que el hecho de que una covarianza sea 0 no implica necesariamente que las variables aleatorias sean estadísticamente independientes se halla en que la covarianza pretende medir una relación lineal y es posible que esta cantidad no detecte otros
tipos de dependencia" Newbold Cap 5

La covarianza dependiendo de su signo si es positivo o negativos indicara si la relacion lineal es directa (creciente) o si es indirecta (negativa)

hay dos tipos de covarianza la poblacion y la muestral que se calculan de la sigiente manera

Cov(x;y) = Σ (xi - μ x) . (yi - μ y) / N (poblacional)

Cov(x;y) = Σ (xi - μ x) . (yi - μ y) / n-1 (muestral)

Coeficiente De Correlacion

En la correlacion buscamos una relacion entre las dos variables que decidimos investigar y uno lo que intenta saber es si hay o no una relacion lineal entre ambas

1

El coeficiente de correlación se calcula dividiendo la covarianza por el producto de las desviaciones típicas de las dos variables.

ρ = COV (x;y) / σX . σY

para variables muestrales se usa la misma formula con la diferencia que se usa el desvio muestral y no se usa ρ sino que se usa r

2

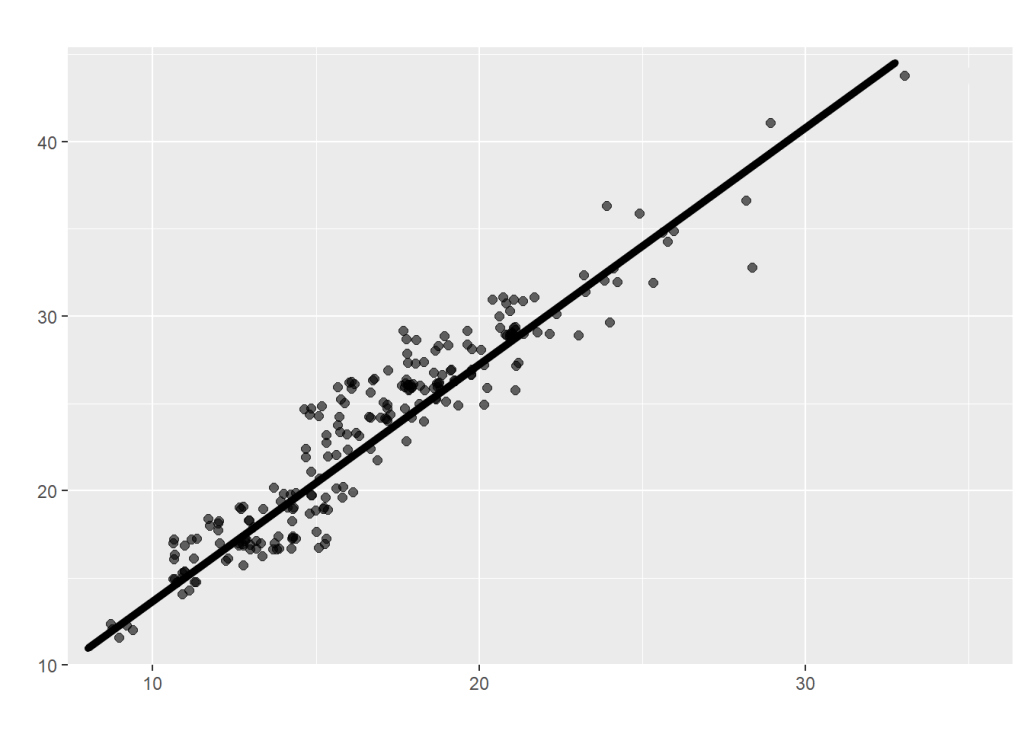
El coeficiente de correlacion va de -1 a 1 , cuanto mas cerca se encuentre r de 1 esa relacion lineal sera de caracter acendente (como la imagen) mientras que cuando r tienda -1 sera de caracter decendente y cuando r=0 significa que no hay una relacion lineal entre las variables

Para calcular r usamos esta formula:

I RI ≥ 2 / √ n

3

En la correlacion me limito al rango de los valores observados es decir que si a mi me dan un valor mayor que el rango que estoy analizando indublamente mi pueba sobre si hay o no relacion lineal no tiene sentido

Prueba de hipotesis para la correlacion

Podemos utilizar la correlación para contrastar la hipótesis de que no existe una relación
lineal o de que exista una relacion lineal

1

Hipotesis nula

cuando la hipotesis nula es igual a 0 significara que no hay relacion lineal entre las variables

2

Hipotesis alternativa

Habra una relacion lineal entre ambas variables cuando se comprueben los siguientes supuestos
H1 ρ > 0
H1 ρ < 0
H1 ρ ≠ 0

3

Utilizaremos la prueba T students

Donde la variable t seguira una distribucion t de students con (n-2) grados de libertad

Covarianza